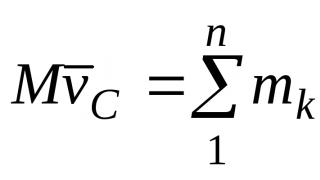Нелинейные колебания. Нелинейные акустические колебания. Смотреть значение Нелинейные Колебания в других словарях

НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ

Нелинейность процессов, в том числе и колебаний, математически выражается в нелинейности соответствующих уравнений движения. С точки зрения физики нелинейность колебаний характеризуется двумя совершенно различными свойствами: ангармоничностью и неизохронностью. Под ангармоничностью понимают наличие в спектре колебаний частот, кратных основной, - Фурье-гармоник, или обертонов. Неизохронными называются колебания, частоты (основной и высших гармоник) которых зависят от амплитуды или энергии колебаний.

Классическим примером нелинейных колебаний может служить обращение планет вокруг Солнца - задача, с решения которой начались современные механика и физика. По третьему закону Кеплера, частота со обращения планет вокруг Солнца задаётся их полной энергией:

w=│E │ 3/2 .

Неизохронность, вообще говоря, не связана с ангармоничностью. Так, заряженная частица, движущаяся по круговой орбите в постоянном магнитном поле со скоростью, близкой к скорости света, совершает колебания чисто гармонические, а частота её обращения обратно пропорциональна энергии.

НЕЛИНЕЙНЫЙ ОСЦИЛЛЯТОР

Линейный (в отсутствие затухания - гармонический) осциллятор - основная модель линейной теории колебаний. Его уравнение движения (по второму закону Ньютона):

где х - величина, колебания которой описывает модель (амплитуда смещения маятника, ток или напряжение в колебательном контуре, численность популяции и т. д.),- её «ускорение».

Нелинейный осциллятор - основная модель нелинейной теории колебаний. Его уравнение движения:

где f (.х ) - нелинейная функция, содержащая по крайней мере один нелинейный (не первой степени по х ) член. Полная энергия системы не зависит от времени, т. е. система консервативна.

Неизохронные колебания совершает, например, частица в плоской потенциальной яме - ящике с бесконечно высокими стенками:

U(x) =0 при - l / 2<х< l / 2; U(х) =¥ при х £- l / 2, х >l / 2.

Частица движется с постоянной скоростью внутри ящика, мгновенно упруго отражаясь на границах. Её кинетическая энергия Е к = mv 2 /2, т. е. скорость V = Ö (2Е к / m ) зависит от энергии. Период колебаний частицы выражается формулой

Из формулы (3) видно, что период колебаний убывает с ростом энергии (для других систем он может возрастать).

Закон сохранения энергии Е осциллятора (консервативной нелинейной системы) имеет вид

Полную качественную картину движения нелинейного осциллятора даёт его фазовый портрет. Из закона сохранения энергии можно вывести

ЛЕОНИД ИСААКОВИЧ МАНДЕЛЬШТАМ

Даже неполный перечень открытий и фундаментальных работ академика Леонида Исааковича Мандельштама (1879-1944) поражает разнообразием: комбинационное и флуктуационное рассеяние света, теория микроскопа, нелинейные колебания и радиотехника, теория резонансов, радиогеодезия, новый вид генераторов электромагнитных волн - параметрические машины. Исключительная, чтобы не сказать болезненная, требовательность Л. И. Мандельштама к результатам работы не позволила включить в этот перечень ряд других, не менее важных открытий, - например, экспериментальное обнаружение в 1912 г. (за несколько лет до классических опытов Стюарта и Толмена) инерции электронов в металлах.

Но за всем впечатляющим разнообразием достижений и широтой интересов в научном творчестве Мандельштама отчётливо прослеживается главная тема - теория колебаний. Впервые познакомившись с этой областью по двухтомной «Теории звука» лорда Рэлея, Мандельштам проникся красотой её идей и неоднократно прибегал к «колебательной помощи», позволявшей находить аналогии между результатами из разных разделов физики.

В Мандельштаме счастливо воплотилось редкое сочетание теоретика и экспериментатора, исследователя и лектора. Он говорил, что существует понимание первого рода, когда читают и понимают всё, что написано, могут вывести любую формулу, но ещё не способны самостоятельно ответить на любой вопрос из прочитанного, и понимание второго рода, когда ясна вся картина, вся связь идей, явлений. Глубокий и тонкий мыслитель, Мандельштам достиг понимания второго рода всей физики и щедро делился знаниями с многочисленными учениками (среди них А. А. Андронов, А. А. Витт, Г. С. Горелик, Г. С. Ландсберг, М. А. Леонтович, В. В. Мигулин, С. М. Рытов, С. П. Стрелков, И. Е. Тамм, С. Э. Хайкин, С. П. Шубин и др.) и студентами.

Родился Мандельштам в Могилёве в семье, давшей миру учёных, врачей и писателей. Вскоре семья переехала в Одессу. До 12 лет мальчик учился дома, затем в гимназии, которую окончил с золотой медалью. В 1897 г. он поступил на математическое отделение физико-математического факультета Новороссийского университета (в Одессе). Через два года в связи со студенческими волнениями юношу исключили из университета. По совету родителей Мандельштам уехал в Страсбург, один из центров физических исследований, где и продолжил образование. В Страсбургском университете тогда преподавали математик Генрих Вебер (ученик Римана и автор классического курса «Дифференциальные уравнения математической физики»), физик Фердинанд Браун (по совместительству директор Физического института), кафедрой теоретической физики заведовал Эмиль Кон (автор известного труда «Электромагнитное поле»).

До сих пор, рассматривая разного типа неустойчивости, мы ограничивали себя только режимами малых амплитуд, когда благодаря возможности линеаризации, сильно упрощается запись и решение дисперсионных уравнений. На самом деле в существующих на практике электронных устройствах в процессе нарастания колебаний, как правило, процессы становятся существенно нелинейными. В качестве немногочисленных исключений можно указать, пожалуй, очень короткоимпульсные или очень короткие вдоль электронного потока электронно-пучковые системы, где колебания не успевают перейти в нелинейную стадию.

Рассматривая особенности нелинейных колебаний, сначала, обратимся к простейшим уравнениям. Вспомним, что линейные колебания автономной одномерной системы без потерь описываются уравнением

Это простейшее уравнение преобразуется к виду, характерному для нелинейных колебаний, если второй член в левой части равенства - нелинейная функция f (x )

(10.5)

Простейший пример нелинейных колебаний - колебания электрона с большой амплитудой в периодическом поле типа показанного на рис.10.1. Такая ситуация реализуется в поле бегущей волны, которая может возникнуть, например, в ЛБВ или ЛОВ .

В
системе координат, движущейся с волной, изменение потенциальной энергии электрона описывается

уравнением

(10.6)

Поэтому уравнение движения электрона может быть записано в виде

так как
и
.

Таким образом, в типичной для СВЧ устройств ситуации движение электрона описывается принципиально нелинейным уравнением. Однако в данном случае проявляется одно из свойств нелинейных систем - их неизохронность , т.е. зависимость их состояния от начальной энергии колеблющейся частицы. Если начальная колебательная энергия электрона мала, он совершает колебательные движения с малой амплитудой вблизи минимума потенциала. В этом случае его движение - практически гармоническое. Если же начальная энергия велика и сравнима с глубиной потенциальной ямы, то амплитуда колебаний тоже велика и в результате движение одновременно становится существенно нелинейным.

Другой отличительной чертой нелинейных колебаний является их негармоничность. Негармоничность нелинейных колебательных поясним подробнее на другом примере.

Пусть мы имеем дело с электронным пучком, распространяющимся вдоль оси x , т.е. движение электронов одномерно. Введем начальную малую по амплитуде модуляцию скорости электронов

, (10.8)

т.е. теперь полная скорость электронов V равна сумме V=V o +u

Введение этого возмущения приводит к тому, что в пучке начнется группировка электронов. Обратим внимание, что рассматриваемая ситуация близка к реализуемой в клистроне, где в резонаторе происходит модуляция по скорости, а в пространстве дрейфа модуляция по скорости преобразуется в модуляцию по плотности.

Рассмотрим эволюцию пучка во времени в системе координат, движущейся с начальной скоростью электронов V o . В этой системе движение обусловлено только начальным возмущением и уравнение движения можно записать в форме

(10.9)

Равенство нулю полной производной возмущения скорости означает, что мы пренебрегаем возникновением электрических сил из-за группировки электронов и ведем рассмотрение без магнитного поля. Конечно, пренебрежение электрическими силами оправдано только на начальной стадии группировки. Затем электрическими полями сгустков уже пренебрегать будет нельзя. Именно эти поля будут ограничивать группировку. Таким образом, мы более-менее корректно можем анализировать только начальный этап эволюции группировки в пучке электронов. Пренебречь действием магнитного поля можно и в том случае, когда оно существует, но ориентировано в направлении движения электронов. При этом однако важно, чтобы электроны не имели поперечных по отношению к силовым линиям магнитного поля скоростей.

Проследим эволюцию характеристик электронного потока, воспользовавшись фазовой плоскостью x,u (рис.10.2). Рассмотрим для начала случай, когда в среде нет дисперсии. В фазовой плоскости каждая точка движется со своей скоростью. Точки верхней полуплоскости движутся вправо, а нижней - влево, причем скорость каждой точки пропорциональна удалению от оси х . Начальное состояние изображено синусоидой (тонкая линия на рисунке 10.2a). Затем синусоида искажается (толстая линия на том же рисунке) и в результате группировки электронов формируются максимумы плотности пространственного заряда вблизи точек, где величина u =0 (рис.10.2b). Одновременно изменение по х скоростей становится негармоническим и формируются сгустки пространственного заряда. Далее появляются точки, где производная стремится к бесконечности, а следовательно и концентрация электронов стремится к бесконечности.

характеристики становятся существенно негармоническими. Это же рассмотрение поясняет условия оптимальной группировки. Такие условия реализуются перед началом опрокидывания волны.

Далеко не при всяких колебаниях возвращающая сила пропорциональна отклонению (т. е. меняется по закону (- кх)). Рассмотрим, например, рессору, изображенную на рисунке 2.74. Она состоит из нескольких пластин. При небольших деформациях изгибаются только длинные пластины. При больших нагрузках изгибу подвергаются и более короткие (и более жесткие) пластины. Возвращающую силу теперь можно описать так:

бательный режим переходит в апериодический, когда колебания исчезают и тело просто медленно приближается к положению равновесия (рис. 2.72, б, в).

Введите вместо строки, где ставятся точки (t,x), строку, где будут ставиться точки (x,v ), и получите фазовые портреты затухающих колебаний при разном трении. Можно воспользоваться и одной из готовых программ Phaspdem* или Phport * из имеющихся в пакете ПАКПРО. Должны получаться диаграммы типа изображенных на рисунке 2.73.

Чтобы она была возвращающей, т. е. F и х всегда имели разные знаки, ее следует разложить в ряд по нечетным степеням х. Поскольку потенциальная энергия U связана с силой формулой F = - dU/dx , это означает, что

т. е. колебания происходят в потенциальной яме со стенками, более крутыми, чем у параболы (рис. 2.75, а). Трение пластин друг о друга обеспечивает затухание, необходимое для демпфирования колебаний.

Возможны колебания и в асимметричной яме, когда

(рис. 2.75, б). Возвращающая сила при этом будет равна

При решении задач на нелинейные колебания неизбежно использование компьютера, так как аналитических решений не существует. На компьютере же решение совсем не сложно. Нужно только в строке, где производится наращивание скорости (v = v + F At/m), полностью написать выражение для F, например -кх- гх 2 - рх 3 .

Пример. Программа для вычерчивания графика нелинейных колебаний приведена в пакете ПАКПРО под именем Nlkol. Запустите ее в работу. Должна получиться серия кривых для разных начальных отклонений. При х 0 большем некоторого значения колеблющаяся частица покидает потенциальную яму, преодолев потенциальный барьер.

Испытайте также работу программ Nlcol* и Nlosc.*, имеющихся в пакете ПАКПРО, а также программы, с помощью которых можно получить фазовые портреты нелинейных колебаний: Phaspnl.*, Phportnl*.

Отметим, что, строго говоря, почти любые колебания являются нелинейными. Только при малых амплитудах их можно считать линейными (пренебрегать членами с х 2 , х 3 и т. д. в формулах типа (2.117)).

Пусть на осциллятор, кроме возвращающей силы, обеспечивающей собственные колебания с частотой С0о, действует еще внешняя сила, причем меняющаяся периодически с частотой со, равной или не равной (Оо. Эта сила будет раскачивать тело с частотой со. Возникающие при этом колебания называются вынужденными.

Уравнение движения в этом случае будет таким:

Вначале происходит процесс установления колебаний. От первого толчка тело начинает колебаться с собственной частотой со 0 . Потом постепенно собственные колебания затухают, и вынуждающая сила начинает управлять процессом. Устанавливаются вынужденные колебания уже не с частотой (Оо, а с частотой вынуждающей силы со. Переходный процесс очень сложен, аналитического решения не существует. При решении задачи численным методом программа будет ничуть не сложнее, чем, скажем, программа для затухающих колебаний. Нужно только в строке, где в соответствии с уравнением движения производится наращивание скорости, добавить вынуждающую силу в виде FobiH = Focos(cot).

Пример. В пакете ПАКГ1РО дан пример программы для получения графика вынужденных колебаний на экране компьютера. См. также программы Ustvcol.pas и UstvcoW.pas. Получающийся график х(?) и фазовая диаграмма v(x) показаны на рисунке 2.76. При удачном подборе параметров хорошо видно, как постепенно устанавливаются вынужденные колебания. Установление вынужденных колебаний интересно наблюдать также на фазовой диаграмме (программа Phpforc.pas).

Когда колебания с частотой со уже установились, можно найти решение уравнения (2.118) в виде

Здесь Жо - амплитуда установившихся колебаний. Если подставить (2.119) в (2.118), найдя предварительно производные по времени х" и х" и учитывая, что к = соо 2 тп, то оказывается, что (2.119) будет решением уравнения (2.118) при условии, что

Трение не учитывалось, коэффициент а полагался равным нулю. Видно, что амплитуда колебаний резко возрастает при приближении со к Сйо (рис. 2.77). Это явление носит название резонанса.

Если бы трения действительно не было, амплитуда при со = (Оо была бы бесконечно большой. Реально так не бывает. На том же рисунке 2.77 показано, как с увеличением трения меняется резонансная кривая. Но все же при совпадении со и соо амплитуда может стать в десятки и сотни раз больше, чем при со Ф СОо. В технике это явление опасно, так как вынуждающие колебания двигателя могут попасть в резонанс с собственной частотой каких-либо частей машины, и она может разрушиться.

Теория нелинейных колебаний начала активно применяться и развиваться в течение последних 50 лет. Основополагающее значение в указанной гипотезе, в частности в концепции автоматических вибраций, принадлежит российскому ученому. М. Ляпунову и его сторонникам, работы которых смогли доказать необходимость использования нелинейных методов в решении сложных задач.

Замечание 1

Теория нелинейных колебаний (или нелинейного механического перемещения частиц среды) направлена на исследование нестабильных колебательных движений, описываемых в физике в виде дифференциальных уравнений.

Данная сфера в механике предоставляет более точное представление о характеристиках вибрационных движений автоматических систем. В итоге линейные формулы получаются путем упрощения нелинейных. Поэтому рассмотрение подобных колебаний дает возможность сделать только определенные заключения о свойствах кратковременных движений, которые могут быть лишь приближенными. Несмотря на это, теория нелинейных вибраций включает важные сведения о систематических решениях, появляющихся за рамками стабильности стационарного состояния.  

Способы проявления нелинейных эффектов

Нелинейные процессы могут формироваться посредством разнообразных методов. Классический и наглядный пример - это нелинейная спираль, в которой возобновляющая сила непосредственно зависит от начального растяжения. В случае параллельной нелинейности (одинаковый итог при растяжении и сжатии) формула движения частиц любого пространства принимает вид:

$\chi + 2 \gamma \chi + \alpha \chi + \beta \chi^3 = f (t)$

Если на систему периодически воздействует внешняя сила, то в классической гипотезе полагают, что и конечный отклик станет цикличным. Резонанс нелинейного явления при малой частоте отклика заключается в его соответствии с плотностью элементов концепции. При постоянном перемещении вынуждающей силы возникает амплитуда соответствующих частот, в котором вероятны разные значения сдвига частиц.

Существуют и другие комплексные решения, такие, как супергармонические и субгармонические вибрации. Если обязывающая сила имеет целостный вид, то другие колебания становятся более высокими. Гипотеза нелинейного резонанса основывается на предположении, что систематическое влияние предполагает создание периодического отклика.

Самоформирующиеся колебания представляют собой иной важный класс нелинейных процессов. Это вибрационные движения, которые формируются в системах без цикличных внешних периодических сил или воздействий.

Парадигма гипотезы нелинейных колебаний

Теория нелинейных движений стала заменой закона электрических вибраций Ван дер Поля. Последняя была генетически взаимосвязана с созданием принципов гипотезы радиотехнического прибора – лампового распределителя. В таком генераторе, функционирующем с определенным «трением» (т.е. будучи неконсервативной концепцией), постепенно появляются незатухающие колебательные перемещения. Это значит, что система включает источник внутренней энергии (или в систему систематически поступает питание извне). Однако в данном аспекте речь не идет о принужденных вибрациях. Ламповое устройство самостоятельно генерирует цикличные самовозбуждающиеся колебания.

Такие процессы возникают и функционируют за счет универсальной конструкции генератора, включающего, кроме колебательного усилитель и контура, связанных с ударной линией обратной связи.

Оставляя нерешенным вопрос о парадигме указанной гипотезы Ван дер Поля, возможно примерно описать концепцию, которая наблюдалась в трудах Мандельштама, Андронова и их последователей в конце 20-х гг.

Замечание 2

В качестве первого и основного элемента в работах ученых выступают «символические обобщения» – математические уравнения, которые определяют и описывают универсальные научные закономерности. В современной физике – это в основном дифференциальные формулы.

Ван дер Поль, в первую очередь, следовал уравнениям, описывающим принцип работы простого лампового распределителя:

$\frac {d^2x}{dt^2} - \mu (1 – 2x^2) \frac {dx}{dt} = x = 0$

Здесь $x$ – общий параметр (в случае генератора – сила и энергия тока), $t$ – определённый период времени, а нелинейный элемент $\frac{x}{dt}$ демонстрирует работу электронной лампы.

Значимую роль в истории теории нелинейных вибраций сыграл так называемый способ припасовывания (позднее названный законом структурно-линейной аппроксимации).

Собственно, в начале 1927 года Мандельштам смог более тщательно проанализировать стабильность колебательных движений, получаемых по указанному принципу. Метод припасовывания и на сегодняшний день широко применяется в гипотезе нелинейных колебаний.

Идеология теории нелинейных процессов

Идеология рассматриваемой гипотезы, прежде всего, характеризует особенности автоколебаний.

Понятия этих явлений были введены Л.В. Андроновым в научных статьях 1928–1929 гг. Фактически с механическими вибрациями имел дело и Ван дер Поль, описывая колебательные движения в ламповом генераторе, но он не так и не смог представить специального термина для них.

В работах Андронова «символическим обобщением» в итоге стало дифференциальное уравнение, по отношению к которому формула Ван дер Поля представляет собой только частный случай. Запись подобной эквивалентности выглядит следующим образом:

$\frac {d^2x}{dt^2} + \frac { 2dx}{dt + \omega^2 x} = f (\frac {x,dx}{dt})$

Идеология появляется вместе с парадигмой, но она распространяется значительно дальше. Идеологические процессы – это выражения и слова, значения которых определяются посредством аналогий, примеров и иллюстраций. Одним из главных признаков использования термина в идеологии является некое размывание его сути. Понятие условно выходит за границы собственной сферы применения.

Пер. с англ. Болдова Б. А. и Гусева Г. Г. Под редакцией В. Е. Боголюбова. - М.: Мир, 1968. - 432 с.
Удк 534 (Механические колебания. Акустика). Есть текстовый слой (т. е. легко копируется текст).
Монография известного японского ученого Т. Хаяси посвящена теории нелинейных колебательных процессов, происходящих в самых различных физических системах.
Книга представляет собой переработанное и дополненное издание одной из более ранних работ автора, знакомой советскому читателю по русскому переводу (Хаяси Т., Вынужденные колебания в нелинейных системах, Ил, М. , 1957). Однако после переработки и дополнения получилась фактически новая книга.
Она отличается от предыдущей не только новыми разделами, но и значительно усовершенствованной методикой изложения. Книга представляет интерес как для физиков и инженеров различных специальностей, имеющих дело с теорией нелинейных колебаний и ее приложениями, так и для математиков, занимающихся теорией дифференциальных уравнений.
Оглавление.
Предисловие к русскому изданию.
Предисловие.
Введение.
Часть i. Основные методы анализа нелинейных колебаний.
Глава i.
Аналитические методы.
Введение.
Метод возмущений.
Метод итераций.
Метод усреднения.
Принцип гармонического баланса.
Численные примеры решения уравнения Дуффинга.
Глава ii.
Топологические методы и графические решения.
Введение.
Интегральные кривые и особые точки на плоскости состояний.
Интегральные кривые и особые точки в пространстве состояний.
Метод изоклин.
Метод Льенара.
Дельта-метод.
Метод наклонных прямых.
Глава iii.
Устойчивость нелинейных систем.
Определение устойчивости по Ляпунову.
Критерий Рауса - Гурвица для нелинейных систем.
Критерий устойчивости по Ляпунову.
Устойчивость периодических колебаний.
Уравнение Матье.
Уравнение Хилла.
Улучшенное приближение характеристического показателя для.
уравнения Хилла.
Часть ii, Вынужденные колебания в установившемся режиме.
Глава iy.
Устойчивость периодических колебаний в системах второго порядка.
Введение.
Условие устойчивости периодических решений.
Улучшенные условия устойчивости.
Дополнительные замечания об условиях устойчивости.
Глава y.
Гармонические колебания.
Гармонические колебания при симметричной нелинейной характеристике.
Гармонические колебания при несимметричной нелинейной характеристике.

Глава Yi.
Ультрагармонические колебания.
Ультрагармонические колебания в.
последовательно-резонансных цепях.
Экспериментальное исследование.
Ультрагармонические колебания в параллельно-резонансных цепях.
Экспериментальное исследование.
Глава Yii.
Субгармонические колебания.
Введение.
Связь между нелинейной характеристикой и порядком.
субгармонических колебаний.

характеристике, представленной кубической функцией.
Субгармонические колебания порядка 1/3 при нелинейной.
характеристике, представленной полиномом пятой степени.
Экспериментальное исследование.

характеристике, представленной полиномом третьей степени.
Субгармонические колебания порядка 1/2 при нелинейной.
характеристике, представленной симметричной квадратичной.
функцией.
Экспериментальное исследование.
Часть iii. Переходные процессы вынужденных колебаний.
Глава Yiii.
Гармонические колебания.
Введение.
Периодические решения и их устойчивость.
Анализ гармонических колебаний с помощью интегральных.
кривых.
Анализ гармонических колебаний на фазовой плоскости.
Геометрический анализ интегральных кривых для консервативных систем.
Геометрический анализ интегральных кривых для диссипативных систем.
Экспериментальное исследование.
Глава ix.
Субгармонические колебания.
Анализ субгармонических колебаний с помощью интегральных кривых.
Анализ субгармонических колебаний порядка 1/3 на фазовой плоскости.
Экспериментальное исследование.
Субгармонические колебания порядка 1/5.
Субгармонические колебания порядка 1/2.
Анализ субгармонических колебаний порядка 1/2 на фазовой.
плоскости.
Исследование на аналоговой вычислительной машине.
Глава x.
Начальные условия, приводящие к различным видам.
периодических колебаний.
Метод анализа.
Симметричные системы.

колебаний порядка 1/3.
Несимметричные системы.
Области притяжения для гармонических и субгармонических.
колебаний порядков 1/2 и 1/3.
Экспериментальные исследования.
Глава Xi.

Введение.
Почти периодические колебания в резонансной цепи с подмагничиванием постоянным током.
Оглавление.
Экспериментальное исследование.
Почти периодические колебания в параметрически.
возбуждаемой цепи.
Часть iv. Автоколебательные системы при периодическом воздействии внешней силы.
Глава Xii.
Захватывание частоты.
Введение.

Гармоническое захватывание.
Ультрагармоническое захватывание.
Субгармоническое захватывание.
Области захватывания частоты.
Анализ при помощи аналоговой вычислительной машины.

Автоколебательная система при нелинейной восстанавливающей силе.
Глава Xiii.
Почти периодические колебания.
Уравнение Ван-дер-Поля с вынуждающим членом.

гармонических колебаний.
Геометрическое рассмотрение интегральных кривых на.
границе гармонического захватывания.
Почти периодические колебания, возникающие из.
ультрагармонических колебаний.
Почти периодические колебания, возникающие из.
субгармонических колебаний.
Автоколебательная система с нелинейной восстанавливающей силой.
Приложение i. Разложения функций Матье.
Приложение ii. Неустойчивые решения уравнения Хилла.
Приложение iii. Неустойчивые решения обобщенного уравнения Хилла.
Приложение iv. Критерий устойчивости, полученный с помощью метода.
возмущений.
Приложение v. Замечания, касающиеся интегральных кривых и особых точек.
Приложение Vi. Электронный синхронный коммутатор.
Задачи.
Литература.
Указатель.
Т. Хаяси.
Нелинейные колебания в физических системах.

Редактор Н. Плужнакова Художник А. Шкловская.
Художественный редактор В. Шаповалов Технический редактор Н. Турсукова.
Сдано в производство 9/Х 1967 г. Подписано к печати 25/Ш 1968 г.
Бумага 60х90у1в-= 13,5 бум. л. 27,0 печ. л.
Уч. -изд. л. 24,
0. Изд. № 1/3899.
Цена 1 р. 91 к. Зак. 907.
Темплан 1968 г. изд-ва «Мир», пор. № 38.
Издательство "Мир", Москва, 1-й Рижский пер. , 2.
Ленинградская типография № 2 имени Евгении Соколовой Главполиграфпрома Комитета.
по печати при Совете Министров Ссср. Измайловский пр. , 29.

Смотрите также

Андрианов И.В., Данишевский В.В., Иванков А.О. Асимптотические методы в теории колебаний балок и пластин

• формат файла: pdf
• размер: 5.53 МБ
• добавлен: 25 сентября 2011 г.

Днепропетровск: Приднепровская государственная академия строительства и архитектуры, 2010 г., 217 с. В монографии рассматриваются асимптотические методы решения задач колебаний балок и пластин. Основное внимание уделено гомотопическому методу возмущений, который основывается на введении искусственного малого параметра. Исследованы линейные колебания конструкций со смешанными граничными условиями, а также нелинейные колебания систем с распределен...

Вибрации в технике. Том 6. Защита от вибрации и ударов

• формат файла: djvu
• размер: 7.28 МБ
• добавлен: 27 октября 2009 г.

Фролов К. В. В шестом томе изложены методы снижения виброактивности источников колебаний и настройки динамических гасителей. Рассмотрены вопросы балансировки вращающихся деталей машин, уравновешивания машин и механизмов, выбора рациональных законов перемещения рабочих органов машин, изоляции оборудования и основания, а также проблемы защиты человека от вибрации. Справочник предназначен для инженерно-технических работников, занятых расчетами, пр...

Ганиев Р.Ф., Кононенко В.О. Колебания твердых тел

• формат файла: djvu
• размер: 8.89 МБ
• добавлен: 27 октября 2011 г.

М.:Наука,1976, 432 с. Исследованы нелинейные колебания в пространственном движении, в частности условия возникновения резонансов. Работа актуальна при создании систем амортизации авиационной и космической техники. Ганиев Р. Ф. - акад. РАН, Кононенко В. О. - акад. АН Украины. Амортизатор упругий 39 Виброамортизация 145, 41, 7 Виброизоляция 145, 417 Возбуждение кинематическое 134, 358 Гирорама двухосная 343 Гирорама трехосная 353 Гироскоп астатичес...

Ден-Гартог Д.П. Механические колебания

• формат файла: djvu
• размер: 7.5 МБ
• добавлен: 25 мая 2010 г.

М. Физматгиз. 1960г. 574 с. Кинематика колебаний. Системы с одной степенью свободы. Две степени свободы. Системы с произвольным числом степеней свободы. Многоцилиндровые двигатели. Вращающиеся части машин. Автоколебания. Квазигармонические и нелинейные колебания систем.

Мигулин В.В. Основы теории колебаний

• формат файла: djvu
• размер: 3.88 МБ
• добавлен: 10 января 2010 г.

Книга знакомит читателя с общими свойствами колебательных процессов, происходящих в радиотехнических, оптических и других системах, а также с различными качественными и количественными методами их изучения. Значительное внимание уделено рассмотрению параметрических, автоколебательных и других нелинейных колебательных систем. Изучение описанных в книге колебательных систем и процессов в них приведено известными методами теории колебаний без подроб...

Обморшев А.Н. Введение в теорию колебаний

• формат файла: pdf
• размер: 8.75 МБ
• добавлен: 23 февраля 2010 г.