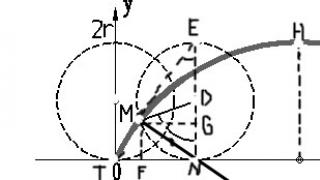
5. Параметрическое уравнение циклоиды и уравнение в декартовых координатах

Допустим, что у нас дана циклоида, образованная окружностью радиуса а с центром в точке А.

Если выбрать в качестве параметра, определяющего положение точки, угол t=∟NDM на который успел повернуться радиус, имевший в начале качения вертикально е положение АО, то координаты х и у точки М выразятся следующим образом:

х= OF = ON - NF = NM - MG = at-a sin t,

y= FM = NG = ND – GD = a – a cos t

Итак параметрические уравнения циклоиды имеют вид:

При изменении t от -∞ до +∞ получится кривая, состоящая из бесчисленного множества таких ветвей, какая изображена на данном рисунке.

Так же, помимо параметрического уравнения циклоиды, существует и ее уравнение в декартовых координатах:

Где r – радиус окружности, образующей циклоиду.

6. Задачи на нахождение частей циклоиды и фигур, образованных циклоидой

Задача №1. Найти площадь фигуры, ограниченной одной аркой циклоиды, уравнение которой задано параметрически

и осью Ох.

Решение. Для решения данной задачи, воспользуемся известными нам фактами из теории интегралов, а именно:

Площадь криволинейного сектора.

Рассмотрим некоторую функцию r = r(ϕ), определенную на [α, β].

ϕ 0 ∈ [α, β] соответствует r 0 = r(ϕ 0) и, значит, точка M 0 (ϕ 0 , r 0), где ϕ 0 ,

r 0 - полярные координаты точки. Если ϕ будет меняться, «пробегая» весь[α, β], то переменная точка M опишет некоторую кривую AB, заданную

уравнением r = r(ϕ).

Определение 7.4. Криволинейным сектором называется фигура, ограниченная двумя лучами ϕ = α, ϕ = β и кривой AB, заданной в полярных

координатах уравнением r = r(ϕ), α ≤ ϕ ≤ β.

Справедлива следующая

Теорема. Если функция r(ϕ) > 0 и непрерывна на [α, β], то площадь

криволинейного сектора вычисляется по формуле:

Эта теорема была доказана ранее в теме определенного интеграла.

Исходя из приведенной выше теоремы, наша задача о нахождении площади фигуры, ограниченной одной аркой циклоиды, уравнение которой задано параметрические x= a (t – sin t) , y= a (1 – cos t) , и осью Ох, сводится к следующему решению.

Решение. Из уравнения кривой dx = a(1−cos t) dt. Первая арка циклоиды соответствует изменению параметра t от 0 до 2π. Следовательно,

Задача №2. Найти длину одной арки циклоиды

Так же в интегральном исчислении изучалась следующая теорема и следствие из нее.

Теорема. Если кривая AB задана уравнением y = f(x), где f(x) и f ’ (x) непрерывны на , то AB является спрямляемой и

Следствие. Пусть AB задана параметрически

L AB = (1)

Пусть функции x(t), y(t) непрерывно-дифференцируемые на [α, β]. Тогда

формулу (1) можно записать так

Сделаем замену переменных в этом интеграле x = x(t), тогда y’(x)= ;

dx= x’(t)dt и, следовательно:

А теперь вернемся к решении нашей задачи.

Решение. Имеем , а поэтому

Задача №3. Надо найти площадь поверхности S, образованной от вращения одной арки циклоиды

L={(x,y): x=a(t – sin t), y=a(1 – cost), 0≤ t ≤ 2π}

В интегральном исчислении существует следующая формула для нахождения площади поверхности тела вращения вокруг оси х кривой, заданной на отрезке параметрически: x=φ(t), y=ψ(t) (t 0 ≤t ≤t 1)

Применяя эту формулу для нашего уравнения циклоиды получаем:

Задача №4. Найти объем тела, полученного при вращении арки циклоиды

Вдоль оси Ох.

В интегральном исчислении при изучении объемов есть следующее замечание:

Если кривая, ограничивающая криволинейную трапецию задана параметрическими уравнениями и функции в этих уравнениях удовлетворяют условиям теоремы о замене переменной в определенном интеграле, то объем тела вращения трапеции вокруг оси Ох, будет вычисляться по формуле

Воспользуемся этой формулой для нахождения нужного нам объема.

Задача решена.

Заключение

Итак, в ходе выполнения данной работы были выяснены основные свойства циклоиды. Так же научились строить циклоиду, выяснила геометрический смысл циклоиды. Как оказалось циклоида имеет огромное практическое применение не только в математике, но и в технологических расчетах, в физике. Но у циклоиды есть и другие заслуги. Ею пользовались ученые XVII века при разработке приемов исследования кривых линий, - тех приемов, которые привели в конце концов к изобретению дифференциального и интегрального исчислений. Она же была одним из «пробных камней», на которых Ньютон, Лейбниц и их первые исследователи испытывали силу новых мощных математических методов. Наконец, задача о брахистохроне привела к изобретению вариационного исчисления, столь нужного физикам сегодняшнего дня. Таким образом, циклоида оказалась неразрывно связанной с одним из самых интересных периодов в истории математики.

Литература

1. Берман Г.Н. Циклоида. – М., 1980

2. Веров С.Г. Брахистохрона, или еще одна тайна циклоиды // Квант. – 1975. - №5

3. Веров С.Г. Тайны циклоиды// Квант. – 1975. - №8.

4. Гаврилова Р.М., Говорухина А.А., Карташева Л.В., Костецкая Г.С.,Радченко Т.Н. Приложения определенного интеграла. Методические указания и индивидуальные задания для студентов 1 курса физического факультета. - Ростов н/Д: УПЛ РГУ, 1994.

5. Гиндикин С.Г. Звездный век циклоиды // Квант. – 1985. - №6.

6. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т.1. – М.,1969

Такая линия и называется «огибающей». Всякая кривая линия есть огибающая своих касательных.

Материя и движение, и тот метод, который они составляют, дают возможность каждому реализовать свои потенциальные возможности в познании истины. Разработка методики развития диалектико-материалистической формы мышления и овладение аналогичным ему методом познания является вторым шагом на пути решения проблемы развития и реализации возможностей Человека. Фрагмент XX Возможности...

Обстановке могут заболеть неврастенией – неврозом, основу клинической картины которого составляет астеническое состояние. И в случае неврастении, и в случае декомпенсации неврастенической психопатии существо душевной (психологической) защиты сказывается уходом от трудностей в раздражительную слабость с вегетативными дисфункциями: либо от нападения человек бессознательно «отбивается»больше...

Различных видах деятельности; развитии пространственного воображения и пространственных представлений, образного, пространственного, логического, абстрактного мышления школьников; формировании умений применять геометро-графические знания и умения для решения различных прикладных задач; ознакомлении с содержанием и последовательностью этапов проектной деятельности в области технического и...

Дуги. Спиралями являются также эвольвенты замкнутых кривых, например эвольвента окружности. Названия некоторым спиралям даны по сходству их полярных уравнений с уравнениями кривых в декартовых координатах, например: · параболическая спираль (а - r)2 = bj, · гиперболическая спираль: r = а/j. · Жезл: r2 = a/j · si-ci-cпираль, параметрические уравнения которой имеют вид: , = , путями .

Иногда кривая определяется с точностью до , то есть с точностью до минимального отношения эквивалентности такого что параметрические кривые

эквивалентны, если существует непрерывная (иногда неубывающая) h из отрезка [a 1 ,b 1 ] на отрезок [a 2 ,b 2 ], такая что

Определяемые этим отношением называются или просто кривыми.

Аналитические определения

В курсах аналитической геометрии доказывается, что среди линий, записываемых в декартовых прямоугольных (или даже в общих аффинных) координатах общим уравнением второй степени

Ax 2 + 2Bxy + Cy 2 + 2Dx + 2Ey + F = 0

(где хотя бы один из коэффициентов A, B, C отличен от нуля) встречаются лишь следующие восемь типов линий:

а) эллипс;

б) гипербола;

в) парабола (невырожденные кривые второго порядка);

г) пара пересекающихся прямых;

д) пара параллельных прямых;

е) пара совпавших прямых (одна прямая);

ж) одна точка (вырожденные линии второго порядка);

з) "линия", совсем не содержащая точек.

Обратно, любая линия каждого из указанных восьми типов записывается в декартовых прямоугольных координатах некоторым уравнением второго порядка. (В курсах аналитической геометрии обычно говорят о девяти (а не о восьми) типах конических сечений, поскольку там различают "мнимый эллипс" и "пару мнимых параллельных прямых", - геометрически эти "линии" одинаковы, поскольку обе не содержат ни одной точки, но аналитически они записываются разными уравнениями.) Поэтому (вырожденные и невырожденные) конические сечения можно определить также как линии второго порядка.

В кривая на плоскости определяется как множество точек, координаты которых удовлетворяют уравнению F ( x , y ) = 0 . При этом на функцию F накладываются ограничения, которые гарантируют, что это уравнение имеет бесконечное множество несовпадающих решений и

это множество решений не заполняет «куска плоскости».

Алгебраические кривые

Важный класс кривых составляют те, для которых функция F ( x , y ) есть от двух переменных. В этом случае кривая, определяемая уравнением F ( x , y ) = 0 , называется .

Алгебраические кривые, задаваемые уравнением 1-й степени, суть .

Уравнение 2-й степени, имеющее бесконечное множество решений, определяет , то есть вырожденные и невырожденные .

Примеры кривых, задаваемых уравнениями 3-ей степени: , .

Примеры кривых 4-ой степени: и .

Пример кривой 6-ой степени: .

Пример кривой, определяемой уравнением чётной степени: (многофокусная) .

Алгебраические кривые, определяемые уравнениями высших степеней, рассматриваются в . При этом большую стройность приобретает их теория, если рассмотрение ведется на . В этом случае алгебраическая кривая определяется уравнением вида

F ( z 1 , z 2 , z 3 ) = 0 ,

где F - многочлен трех переменных, являющихся точек.

Типы кривых

Плоская кривая - кривая, все точки которой лежат в одной плоскости.

(простая линия или жорданова дуга, также контур) - множество точек плоскости или пространства, находящихся во взаимно однозначном и взаимно непрерывном соответствии с отрезками прямой.

Путь - отрезка в .

аналитические кривые, не являющиеся алгебраическими. Более точно - кривые, которые можно задать через линию уровня аналитической функции (или, в многомерном случае, системы функций).

Синусоида,

Циклоида,

Спираль Архимеда,

Трактриса,

Цепная линия,

Гиперболическая спираль и др.

1. Способы задания кривых:

аналитический – кривая задана математическим уравнением;

графический – кривая задана визуально на носителе графической информации;

табличный – кривая задана координатами последовательного ряда точек.

параметрический (наиболее общий способ задать уравнение кривой) :

где - гладкие функции параметра t , причем

(x ") 2 + (y ") 2 + (z ") 2 > 0 (условие регулярности).

Часто удобно использовать инвариантную и компактную запись уравнения кривой с помощью :

где в левой части стоит точек кривой, а правая определяет его зависимость от некоторого параметра t . Раскрыв эту запись в координатах, мы получаем формулу (1).

1. Циклоида.

История исследования циклоиды связана с именами таких великих учёных, философов, математиков и физиков, как Аристотель, Птолемей, Галилей, Гюйгенс, Торричелли и др.

Циклоида (от κυκλοειδής - круглый) - , которую можно определить как траекторию точки, лежащей на границе круга, катящегося без скольжения по прямой. Эту окружность называют порождающей.

Одним из древнейших способов образования кривых является кинематический способ, при котором кривая получается как траектория движения точки. Кривая, которая получается как траектория движения точки, закрепленной на окружности, катящейся без скольжения по прямой, по окруж­ности или другой кривой, называется циклоидальной, что в переводе с греческого языка означает кругообразная, напоминающая о круге.

Рассмотрим сначала случай, когда окружность катится по прямой. Кривая, которую описывает точка, закрепленная на окружности, катящейся без скольжения по прямой линии, называется циклоидой.

Пусть окружность радиуса R катится по прямой а. С – точка, закрепленная на окружности, в начальный момент времени находящаяся в по­ложении А (рис. 1). Отложим на прямой а отрезок АВ, равный длине окружности, т.е. АВ = 2 π R. Разделим этот отрезок на 8 равных частей точками А1, А2, ..., А8 = В.

Ясно, что когда окружность, катясь по прямой а, сделает один оборот, т.е. повернется на 360, то она займет положение (8), а точка С переместится из положения А в положение В.

Если окружность сделает половину полного оборота, т.е. повернется на 180, то она займет положение (4), а точка С переместится в самое верхнее положение С4.

Если окружность повернется на угол 45, то окружность переместится в положение (1), а точка С переместится в положение С1.

На рисунке 1 показаны также другие точки циклоиды, соответствующие оставшимся углам поворота окружности, кратным 45.

Соединяя плавной кривой построенные точки, получим участок циклоиды, соответствующий одному полному обороту окружности. При следующих оборотах будут получаться такие же участки, т.е. циклоида будет состоять из периодически повторяющегося участка, называемого аркой циклоиды.

Обратим внимание на положение касательной к циклоиде (рис. 2). Если велосипедист едет по мокрой дороге, то оторвавшиеся от колеса капли будут лететь по касательной к циклоиде и при отсутствии щитков могут забрызгать спину велосипедиста.

Первым, кто стал изучать циклоиду, был Галилео Галилей (1564 – 1642). Он же придумал и ее название.

Свойства циклоиды:

Циклоида обладает целым рядом замечательных свойств. Упомянем о некоторых из них.

Свойство 1. (Ледяная гора.) В 1696 году И.Бернулли поставил задачу о нахождении кривой наискорейшего спуска, или, иначе говоря, задачу о том, какова должна быть форма ледяной горки, чтобы, скатываясь по ней, совершить путь из начальной точки А в конечную точку В за кратчайшее время (рис. 3, а). Искомую кривую назвали "брахистохроной", т.е. кривой кратчайшего времени.

Ясно, что кратчайшим путем из точки A в точку B является отрезок AB. Однако при таком прямолинейном движении скорость набирается медленно и затраченное на спуск время оказывается большим (рис. 3, б).

Скорость набирается тем быстрее, чем круче спуск. Однако при крутом спуске удлиняется путь по кривой и тем самым увеличивается время его прохождения.

Среди математиков, решавших эту задачу, были: Г.Лейбниц, И.Ньютон, Г.Лопиталь и Я.Бернулли. Они доказали, что искомой кривой является перевернутая циклоида (рис. 3, а). Методы, развитые этими учеными при решении задачи о брахистохроне, положили начало новому направлению математики - вариационному исчислению.

Свойство 2. (Часы с маятником.) Часы с обычным маятником не могут идти точно, поскольку период колебаний маятника зависит от его амплитуды: чем больше амплитуда, тем больше период. Голландский ученый Христиан Гюйгенс (1629 – 1695) задался вопросом, по какой кривой должен двигаться шарик на нитке маятника, чтобы период его колебаний не зависел от амплитуды. Заметим, что в обычном маятнике кривой, по которой движется шарик, является окружность (рис. 4).

Искомой кривой оказалась перевернутая циклоида. Если, например, в форме перевернутой циклоиды изготовить желоб и пустить по нему шарик, то период движения шарика под действием силы тяжести не будет зависеть от начального его положения и от амплитуды (рис. 5). За это свойство циклоиду называют также "таутохрона" – кривая равных времен.

Гюйгенс изготовил две деревянные дощечки с краями в форме циклоиды, ограничивающие движение нити слева и справа (рис. 6). При этом сам шарик будет двигаться по перевернутой циклоиде и, таким образом, период его колебаний не будет зависеть от амплитуды.

Из этого свойства циклоиды, в частности следует, что независимо от того, с какого места ледяной горки в форме перевернутой циклоиды мы начнем спуск, на весь путь до конечной точки мы затратим одно и то же время.

Уравнение циклоиды

1.Уравнение циклоиды удобно записывать через α – угол поворота окружности, выраженный в радианах, заметим, что α также равняется пути, пройденному производящей окружностью по прямой.

x=rα – r sin α

y=r – r cos α

2.Примем горизонтальную ось координат в качестве прямой, по которой катится производящая окружность радиуса r .

Циклоида описывается параметрическими уравнениями

x = rt – r sin t ,

y = r – r cos t .

Уравнение в :

Циклоида может быть получена как решение дифференциального уравнения:

Из истории о циклоиде

Первым из учёных обратил внимание на циклоиду в , но серьёзное исследование этой кривой началось только в .

Первым, кто стал изучать циклоиду, был Галилео Галилей (1564-1642) – знаменитый итальянский астроном, физик и просветитель. Он же придумал название «циклоида», что значит: «напоминающая о круге». Сам Галилей о циклоиде ничего не писал, но о его работах в этом направлении упоминают ученики и последователи Галилея: Вивиани, Торичелли и другие. Торичелли – известный физик, изобретатель барометра – уделял немало времени и математике. В эпоху Возрождения не было узких ученых-специалистов. Талантливый человек занимался и философией, и физикой, и математикой и всюду получал интересные результаты и делал крупные открытия. Немного позже итальянцев за циклоиду принялись французы, назвавшие её «рулеттой» или «трохоидой». В 1634 году Роберваль – изобретатель известной системы весов системы весов – вычислил площадь, ограниченную аркой циклоиды и её основанием. Содержательное исследование циклоиды провёл современник Галилея . Среди , то есть кривых, уравнение которых не может быть записано в виде от x , y , циклоида - первая из исследуемых.

Писал о циклоиде:

Рулетта является линией столь обычной, что после прямой и окружности нет более часто встречающейся линии; она так часто вычерчивается перед глазами каждого, что надо удивляться тому, как не рассмотрели её древние… ибо это не что иное, как путь, описываемый в воздухе гвоздём колеса.

Новая кривая быстро завоевала популярность и подверглась глубокому анализу, в котором участвовали , , Ньютон, , братья Бернулли и другие корифеи науки XVII-XVIII веков. На циклоиде активно оттачивались методы появившегося в те годы . Тот факт, что аналитическое исследование циклоиды оказалось столь же успешным, как и анализ алгебраических кривых, произвёл большое впечатление и стал важным аргументом в пользу «уравнения в правах» алгебраических и трансцендентных кривых. Эпициклоида

Некоторые виды циклоид

Эпициклоида - траектория точки А, лежащей на окружности диаметра D, которая катится без скольжения по направляющей окружности радиуса R (касание внешнее).

Построение эпициклоиды выполняется в следующей последовательности:

Из центра 0 проводят вспомогательную дугу радиусом равным 000=R+r;

Из точек 01, 02, ...012, как из центров, проводят окружности радиуса r до пересечения с вспомогательными дугами в точках А1, А2, ... А12, которые принадлежат эпициклоиде.

Гипоциклоида

Гипоциклоида - траектория точки А, лежащей на окружности диаметра D, которая катится без скольжения по направляющей окружности радиуса R (касание внутреннее).

Построение гипоциклоиды выполняется в следующей последовательности:

Производящую окружность радиуса r и направляющую окружность радиуса R проводят так, чтобы они касались в точке А;

Производящую окружность делят на 12 равных частей, получают точки 1, 2, ... 12;

Из центра 0 проводят вспомогательную дугу радиусом равным 000=R-r;

Центральный угол a определяют по формуле a =360r/R.

Делят дугу направляющей окружности, ограниченную углом a, на 12 равных частей, получают точки 11, 21, ...121;

Из центра 0 через точки 11, 21, ...121 проводят прямые до пересечения с вспомогательной дугой в точках 01, 02, ...012;

Из центра 0 проводят вспомогательные дуги через точки деления 1, 2, ... 12 производящей окружности;

Из точек 01, 02, ...012, как из центров, проводят окружности радиуса r до пересечения с вспомогательными дугами в точках А1, А2, ... А12, которые принадлежат гипоциклоиде.

1. Кардиоида.

Кардиоида ( καρδία - сердце, Кардиоида является частным случаем Термин «кардиоида» введен Кастиллоном в 1741 году.

Если взять окружность и в качестве полюса точку на ней, то кардиоиду получим только в том случае, если откладывать отрезки, равные диаметру окружности. При других величинах откладываемых отрезков конхоидами будут удлиненные или укороченные кардиоиды. Эти удлиненные и укороченные кардиоиды называются иначе улитками Паскаля.

Кардиоида имеет различные применения в технике. В форме кардиоиды делают эксцентрики, кулачки у машин. Ею пользуются иногда при вычерчивании зубчатых колес. Кроме того, она применяется в оптической технике.

Свойства кардиоиды

Кардиоида - В М на подвижной окружности будет описывать замкнутую траекторию. Эта плоская кривая называется кардиоидой.

2)Кардиоиду можно получить и другим способом. Отметим на окружности точку О и проведем из нее луч. Если от точки А пересечения этого луча с окружностью отложить отрезок АМ, по длине равный диаметру окружности, и луч вращать вокруг точки О , то точка М будет двигаться по кардиоиде.

3)Кардиоида может быть также представлена как кривая, касающаяся всех окружностей, имеющих центры на данной окружности и проходящих через ее фиксированную точку. Когда построены несколько окружностей, кардиоида оказывается построенной как бы сама собой.

4)Есть еще столь же изящный, сколь, неожиданный способ увидеть кардиоиду. На рисунке можно увидеть точечный источник света на окружности. После того как лучи света отразятся в первый раз от окружности, они идут по касательной к кардиоиде. Представьте себе теперь, что окружность – это края чашки, в одной точке ее отражается яркая лампочка. В чашку налит черный кофе, позволяющий увидеть яркие отраженные лучи. Кардиоида в результате оказывается выделенной лучами света.

1. Астроида.

Астроида (от греч. astron - звезда и eidos - вид), плоская кривая, описываемая точкой окружности, которая касается изнутри неподвижной окружности вчетверо большего радиуса и катится по ней без скольжения. Принадлежит к гипоциклоидам. Астроида - алгебраическая кривая 6-го порядка.

Астроида.

Длина всей астроиды равна шести радиусам неподвижного круга, а площадь, ею ограниченная,- трем восьмым неподвижного круга.

Отрезок касательной к астроиде, заключенный между двумя взаимно перпендикулярными радиусами неподвижного круга, проведенными в острия астроиды, равен радиусу неподвижного круга, независимо от того, как была выбрана точка.

Свойства астроиды

Имеются четыре каспа .

Длина дуги от точки с 0 до огибающей

семейства отрезков постоянной длины, концы которых расположены на двух взаимно перпендикулярных прямых.

Астроида является 6-го порядка.

Уравнения астроиды

Уравнение в декартовых прямоугольных координатах: | x | 2 / 3 + | y | 2 / 3 = R 2 / 3 параметрическое уравнение: x = Rcos 3 t y = Rsin 3 t

Способ построения астроиды

Чертим две взаимно перпендикулярные прямые и проводим ряд отрезков длиною R , концы которых лежат на этих прямых. На рисунке изображено 12 таких отрезков (включая отрезки самих взаимно перпендикулярных прямых). Чем больше проведем отрезков, тем точнее получим кривую. Построим теперь огибающую всех этих отрезков. Этой огибающей будет астроида.

1. Заключение

В работе приведены примеры задач с различными видами кривых, определяемых различными уравнениями или удовлетворяющих некоторому математическому условию. В частности циклоидальные кривые, способы их задания, различные способы построения, свойства этих кривых.

Свойства циклоидальных кривых очень часто используется в механике в зубчатых передачах, что существенно повышает прочность деталей в механизмах.

Помни-те оран-же-вые пласт-мас-со-вые ка-та-фо-ты - све-то-от-ра-жа-те-ли, при-креп-ля-ю-щи-е-ся к спи-цам ве-ло-си-пед-но-го ко-ле-са? При-кре-пим ка-та-фот к са-мо-му обо-ду ко-ле-са и про-сле-дим за его тра-ек-то-ри-ей . По-лу-чен-ные кри-вые при-над-ле-жат се-мей-ству цик-ло-ид.

Ко-ле-со при этом на-зы-ва-ет-ся про-из-во-дя-щим кру-гом (или окруж-но-стью) цик-ло-и-ды.

Но да-вай-те вер-нём-ся в наш век и пе-ре-ся-дем на бо-лее совре-мен-ную тех-ни-ку. На пу-ти бай-ка по-пал-ся ка-му-шек, ко-то-рый за-стрял в про-тек-то-ре ко-ле-са. Про-вер-нув-шись несколь-ко кру-гов с ко-ле-сом, ку-да по-ле-тит ка-мень, ко-гда вы-ско-чит из про-тек-то-ра? Про-тив на-прав-ле-ния дви-же-ния мо-то-цик-ла или по на-прав-ле-нию?

Как из-вест-но, сво-бод-ное дви-же-ние те-ла на-чи-на-ет-ся по ка-са-тель-ной к той тра-ек-то-рии, по ко-то-рой оно дви-га-лось. Ка-са-тель-ная к цик-ло-и-де все-гда на-прав-ле-на по на-прав-ле-нию дви-же-ния и про-хо-дит через верх-нюю точ-ку про-из-во-дя-щей окруж-но-сти. По на-прав-ле-нию дви-же-ния по-ле-тит и наш ка-му-шек.

Помни-те, как Вы ка-та-лись в дет-стве по лу-жам на ве-ло-си-пе-де без зад-не-го кры-ла? Мок-рая по-лос-ка на ва-шей спине яв-ля-ет-ся жи-тей-ским под-твер-жде-ни-ем толь-ко что по-лу-чен-но-го ре-зуль-та-та.

Век XVII - это век цик-ло-и-ды. Луч-шие учё-ные изу-ча-ли её уди-ви-тель-ные свой-ства.

Ка-кая тра-ек-то-рия при-ве-дёт те-ло, дви-жу-ще-е-ся под дей-стви-ем си-лы тя-же-сти, из од-ной точ-ки в дру-гую за крат-чай-шее вре-мя ? Это бы-ла од-на из пер-вых за-дач той на-у-ки, ко-то-рая сей-час но-сит на-зва-ние ва-ри-а-ци-он-ное ис-чис-ле-ние.

Ми-ни-ми-зи-ро-вать (или мак-си-ми-зи-ро-вать) мож-но раз-ные ве-щи - дли-ну пу-ти, ско-рость, вре-мя. В за-да-че о бра-хи-сто-хроне ми-ни-ми-зи-ру-ет-ся имен-но вре-мя (что под-чёр-ки-ва-ет-ся са-мим на-зва-ни-ем: греч. βράχιστος - наи-мень-ший, χρόνος - вре-мя).

Пер-вое, что при-хо-дит на ум, - это пря-мо-ли-ней-ная тра-ек-то-рия. Да-вай-те так-же рас-смот-рим пе-ре-вёр-ну-тую цик-ло-и-ду с точ-кой воз-вра-та в верх-ней из за-дан-ных то-чек. И, сле-дуя за Га-ли-лео Га-ли-ле-ем, - чет-вер-тин-ку окруж-но-сти , со-еди-ня-ю-щую на-ши точ-ки.

По-че-му же Га-ли-лео Га-ли-лей рас-смат-ри-вал чет-вер-тин-ку окруж-но-сти и счи-тал, что это наи-луч-шая в смыс-ле вре-ме-ни тра-ек-то-рия спус-ка? Он впи-сы-вал в неё ло-ма-ные и за-ме-тил, что при уве-ли-че-нии чис-ла зве-ньев вре-мя спус-ка умень-ша-ет-ся. От-сю-да Га-ли-лей есте-ствен-ным об-ра-зом пе-ре-шёл к окруж-но-сти, но сде-лал невер-ный вы-вод, что эта тра-ек-то-рия наи-луч-шая сре-ди всех воз-мож-ных. Как мы ви-де-ли, наи-луч-шей тра-ек-то-ри-ей яв-ля-ет-ся цик-ло-и-да.

Через две дан-ные точ-ки мож-но про-ве-сти един-ствен-ную цик-ло-и-ду с усло-ви-ем, что в верх-ней точ-ке на-хо-дит-ся точ-ка воз-вра-та цик-ло-и-ды. И да-же ко-гда цик-ло-и-де при-хо-дит-ся под-ни-мать-ся, чтобы прой-ти через вто-рую точ-ку, она всё рав-но бу-дет кри-вой наи-ско-рей-ше-го спус-ка !

Ещё од-на кра-си-вая за-да-ча, свя-зан-ная с цик-ло-и-дой, - за-да-ча о та-у-то-хроне. В пе-ре-во-де с гре-че-ско-го ταύτίς озна-ча-ет «тот же са-мый», χρόνος, как мы уже зна-ем - «вре-мя».

Сде-ла-ем три оди-на-ко-вые гор-ки с про-фи-лем в ви-де цик-ло-и-ды, так, чтобы кон-цы го-рок сов-па-да-ли и рас-по-ла-га-лись в вер-шине цик-ло-и-ды . По-ста-вим три бо-ба на раз-ные вы-со-ты и да-дим от-маш-ку. Уди-ви-тель-ней-ший факт - все бо-бы при-едут вниз од-новре-мен-но !

Зи-мой Вы мо-же-те по-стро-ить во дво-ре гор-ку изо льда и про-ве-рить это свой-ство вжи-вую.

За-да-ча о та-у-то-хроне со-сто-ит в на-хож-де-нии та-кой кри-вой, что, на-чи-ная с лю-бо-го на-чаль-но-го по-ло-же-ния, вре-мя спус-ка в за-дан-ную точ-ку бу-дет оди-на-ко-вым.

Хри-сти-ан Гюй-генс до-ка-зал, что един-ствен-ной та-у-то-хро-ной яв-ля-ет-ся цик-ло-и-да.

Ко-неч-но же, Гюй-ген-са не ин-те-ре-со-вал спуск по ле-дя-ным гор-кам. В то вре-мя учё-ные не име-ли та-кой рос-ко-ши за-ни-мать-ся на-у-ка-ми из люб-ви к ис-кус-ству. За-да-чи, ко-то-рые изу-ча-лись, ис-хо-ди-ли из жиз-ни и за-про-сов тех-ни-ки то-го вре-ме-ни. В XVII ве-ке со-вер-ша-ют-ся уже даль-ние мор-ские пла-ва-ния. Ши-ро-ту мо-ря-ки уме-ли опре-де-лять уже до-ста-точ-но точ-но, но уди-ви-тель-но, что дол-го-ту не уме-ли опре-де-лять со-всем. И один из пред-ла-гав-ших-ся спо-со-бов из-ме-ре-ния ши-ро-ты был ос-но-ван на на-ли-чии точ-ных хро-но-мет-ров.

Пер-вым, кто за-ду-мал де-лать ма-ят-ни-ко-вые ча-сы, ко-то-рые бы-ли бы точ-ны, был Га-ли-лео Га-ли-лей. Од-на-ко в тот мо-мент, ко-гда он на-чи-на-ет их ре-а-ли-зо-вы-вать, он уже стар, он слеп, и за остав-ший-ся год сво-ей жиз-ни учё-ный не успе-ва-ет сде-лать ча-сы. Он за-ве-ща-ет это сы-ну, од-на-ко тот мед-лит и на-чи-на-ет за-ни-мать-ся ма-ят-ни-ком то-же лишь пе-ред смер-тью и не успе-ва-ет ре-а-ли-зо-вать за-мы-сел. Сле-ду-ю-щей зна-ко-вой фигу-рой был Хри-сти-ан Гюй-генс.

Он за-ме-тил, что пе-ри-од ко-ле-ба-ния обыч-но-го ма-ят-ни-ка, рас-смат-ри-вав-ше-го-ся Га-ли-ле-ем, за-ви-сит от из-на-чаль-но-го по-ло-же-ния, т.е. от ам-пли-ту-ды. За-ду-мав-шись о том, ка-ко-ва долж-на быть тра-ек-то-рия дви-же-ния гру-за, чтобы вре-мя ка-че-ния по ней не за-ви-се-ло от ам-пли-ту-ды, он ре-ша-ет за-да-чу о та-у-то-хроне. Но как за-ста-вить груз дви-гать-ся по цик-ло-и-де ? Пе-ре-во-дя тео-ре-ти-че-ские ис-сле-до-ва-ния в прак-ти-че-скую плос-кость, Гюй-генс де-ла-ет «щёч-ки», на ко-то-рые на-ма-ты-ва-ет-ся ве-рев-ка ма-ят-ни-ка, и ре-ша-ет ещё несколь-ко ма-те-ма-ти-че-ских за-дач. Он до-ка-зы-ва-ет, что «щёч-ки» долж-ны иметь про-филь той же са-мой цик-ло-и-ды, тем са-мым по-ка-зы-вая, что эво-лю-той цик-ло-и-ды яв-ля-ет-ся цик-ло-и-да с те-ми же па-ра-мет-ра-ми.

Кро-ме то-го, пред-ло-жен-ная Гюй-ген-сом кон-струк-ция цик-ло-и-даль-но-го ма-ят-ни-ка поз-во-ля-ет по-счи-тать дли-ну цик-ло-и-ды. Ес-ли си-нюю ни-точ-ку, дли-на ко-то-рой рав-на че-ты-рём ра-ди-у-сам про-из-во-дя-ще-го кру-га, мак-си-маль-но от-кло-нить, то её ко-нец бу-дет в точ-ке пе-ре-се-че-ния «щёч-ки» и цик-ло-и-ды-тра-ек-то-рии, т.е. в вер-шине цик-ло-и-ды-«щёч-ки». Так как это по-ло-ви-на дли-ны ар-ки цик-ло-и-ды, то пол-ная дли-на рав-на вось-ми ра-ди-у-сам про-из-во-дя-ще-го кру-га.

Хри-сти-ан Гюй-генс сде-лал цик-ло-и-даль-ный ма-ят-ник, и ча-сы с ним про-хо-ди-ли ис-пы-та-ния в мор-ских пу-те-ше-стви-ях, но не при-жи-лись. Впро-чем, так же, как и ча-сы с обыч-ным ма-ят-ни-ком для этих це-лей.

От-че-го же, од-на-ко, до сих пор су-ще-ству-ют ча-со-вые ме-ха-низ-мы с обык-но-вен-ным ма-ят-ни-ком? Ес-ли при-гля-деть-ся, то при ма-лых от-кло-не-ни-ях, как у крас-но-го ма-ят-ни-ка, «щёч-ки» цик-ло-и-даль-но-го ма-ят-ни-ка по-чти не ока-зы-ва-ют вли-я-ния. Со-от-вет-ствен-но, дви-же-ние по цик-ло-и-де и по окруж-но-сти при ма-лых от-кло-не-ни-ях по-чти сов-па-да-ют.